




Cyclomatic complexity (or conditional complexity) is a software metric (measurement). It was developed by Thomas J. McCabe, Sr. in 1976 and is used to indicate the complexity of a program. It directly measures the number of linearly independent paths through a program's source code. The concept, although not the method, is somewhat similar to that of general text complexity measured by the Flesch-Kincaid Readability Test.
Cyclomatic complexity is computed using the control flow graph of the program: the nodes of the graph correspond to indivisible groups of commands of a program, and a directed edge connects two nodes if the second command might be executed immediately after the first command. Cyclomatic complexity may also be applied to individual functions, modules, methods or classes within a program.
One testing strategy, called Basis Path Testing by McCabe who first proposed it, is to test each linearly independent path through the program; in this case, the number of test cases will equal the cyclomatic complexity of the program.[1]

The cyclomatic complexity of a section of source code is the count of the number of linearly independent paths through the source code. For instance, if the source code contained no decision points such as IF statements or FOR loops, the complexity would be 1, since there is only a single path through the code. If the code had a single IF statement containing a single condition there would be two paths through the code, one path where the IF statement is evaluated as TRUE and one path where the IF statement is evaluated as FALSE.
Mathematically, the cyclomatic complexity of a structured program[note 1] is defined with reference to a directed graph containing the basic blocks of the program, with an edge between two basic blocks if control may pass from the first to the second (the control flow graph of the program). The complexity is then defined as:[2]
where

An alternative formulation is to use a graph in which each exit point is connected back to the entry point. In this case, the graph is said to be strongly connected, and the cyclomatic complexity of the program is equal to the cyclomatic number of its graph (also known as the first Betti number), which is defined as:[2]
This may be seen as calculating the number of linearly independent cycles that exist in the graph, i.e. those cycles that do not contain other cycles within themselves. Note that because each exit point loops back to the entry point, there is at least one such cycle for each exit point.
For a single program (or subroutine or method), P is always equal to 1. Cyclomatic complexity may, however, be applied to several such programs or subprograms at the same time (e.g., to all of the methods in a class), and in these cases P will be equal to the number of programs in question, as each subprogram will appear as a disconnected subset of the graph.
It can be shown that the cyclomatic complexity of any structured program with only one entrance point and one exit point is equal to the number of decision points (i.e., 'if' statements or conditional loops) contained in that program plus one.[2][3]
Cyclomatic complexity may be extended to a program with multiple exit points; in this case it is equal to:
where π is the number of decision points in the program, and s is the number of exit points.[3][4]
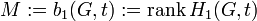 |
which is read as “the first homology of the graph G, relative to the terminal nodes t”. This is a technical way of saying “the number of linearly independent paths through the flow graph from an entry to an exit”, where:
This corresponds to the intuitive notion of cyclomatic complexity, and can be calculated as above.
Alternatively, one can compute this via absolute Betti number
(absolute homology – not relative) by identifying (gluing together) all
terminal nodes on a given component (or equivalently, draw paths
connecting the exits to the entrance), in which case (calling the new,
augmented graph 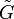 ,
which is ), one obtains:
,
which is ), one obtains:
This corresponds to the characterization of cyclomatic complexity as “number of loops plus number of components”.
The name Cyclomatic Complexity is motivated by the number of different cycles in the program control flow graph, after having added an imagined branch back from the exit node to the entry node.[2]
One of McCabe's original applications was to limit the complexity of routines during program development; he recommended that programmers should count the complexity of the modules they are developing, and split them into smaller modules whenever the cyclomatic complexity of the module exceeded 10.[2] This practice was adopted by the NIST Structured Testing methodology, with an observation that since McCabe's original publication, the figure of 10 had received substantial corroborating evidence, but that in some circumstances it may be appropriate to relax the restriction and permit modules with a complexity as high as 15. As the methodology acknowledged that there were occasional reasons for going beyond the agreed-upon limit, it phrased its recommendation as: "For each module, either limit cyclomatic complexity to [the agreed-upon limit] or provide a written explanation of why the limit was exceeded."[5]
Another application of cyclomatic complexity is in determining the number of test cases that are necessary to achieve thorough test coverage of a particular module.
It is useful because of two properties of the cyclomatic complexity, M, for a specific module:
All three of the above numbers may be equal: branch coverage 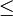 cyclomatic complexity
cyclomatic complexity 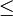 number of paths.
number of paths.
For example, consider a program that consists of two sequential if-then-else statements.
if( c1() )
f1();
else
f2();
if( c2() )
f3();
else
f4();
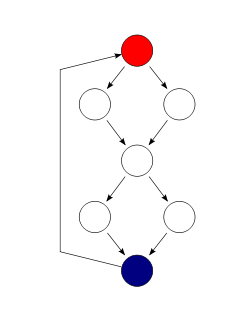
In this example, two test cases are sufficient to achieve a complete branch coverage, while four are necessary for complete path coverage. The cyclomatic complexity of the program is 3 (as the strongly-connected graph for the program contains 9 edges, 7 nodes and 1 connected component).
In general, in order to fully test a module all execution paths through the module should be exercised. This implies a module with a high complexity number requires more testing effort than a module with a lower value since the higher complexity number indicates more pathways through the code. This also implies that a module with higher complexity is more difficult for a programmer to understand since the programmer must understand the different pathways and the results of those pathways.
Unfortunately, it is not always practical to test all possible paths through a program. Considering the example above, each time an additional if-then-else statement is added, the number of possible paths doubles. As the program grew in this fashion, it would quickly reach the point where testing all of the paths was impractical.
One common testing strategy, espoused for example by the NIST Structured Testing methodology, is to use the cyclomatic complexity of a module to determine the number of white-box tests that are required to obtain sufficient coverage of the module. In almost all cases, according to such a methodology, a module should have at least as many tests as its cyclomatic complexity; in most cases, this number of tests is adequate to exercise all the relevant paths of the function.[5]
As an example of a function that requires more than simply branch coverage to test accurately, consider again the above function, but assume that to avoid a bug occurring, any code that calls either f1() or f3() must also call the other.[note 2] Assuming that the results of c1() and c2() are independent, that means that the function as presented above contains a bug. Branch coverage would allow us to test the method with just two tests, and one possible set of tests would be to test the following cases:
Neither of these cases exposes the bug. If, however, we use cyclomatic complexity to indicate the number of tests we require, the number increases to 3. We must therefore test one of the following paths:
Either of these tests will expose the bug.
One would also expect that a module with higher complexity would tend to have lower cohesion (less than functional cohesion) than a module with lower complexity. The possible correlation between higher complexity measure with a lower level of cohesion is predicated on a module with more decision points generally implementing more than a single well defined function. A 2005 study showed stronger correlations between complexity metrics and an expert assessment of cohesion in the classes studied than the correlation between the expert's assessment and metrics designed to calculate cohesion.[6]
A number of studies have investigated cyclomatic complexity's correlation to the number of defects contained in a module. Most such studies find a strong positive correlation between cyclomatic complexity and defects: modules that have the highest complexity tend to also contain the most defects. For example, a 2008 study by metric-monitoring software supplier Enerjy analyzed classes of open-source Java applications and divided them into two sets based on how commonly faults were found in them. They found strong correlation between cyclomatic complexity and their faultiness, with classes with a combined complexity of 11 having a probability of being fault-prone of just 0.28, rising to 0.98 for classes with a complexity of 74.[7]
However, studies that control for program size (i.e., comparing modules that have different complexities but similar size, typically measured in lines of code) are generally less conclusive, with many finding no significant correlation, while others do find correlation. Some researchers who have studied the area question the validity of the methods used by the studies finding no correlation.[8]
Many tools count Cyclomatic Complexity differently from each other, as there are different approaches to what code generates a new execution path (a node). ProjectCodeMeter counts statements according to their effective function, not strictly the keyword. The general guiding rule is to give the same cyclomatic count to codes with the same functionality, regardless or the way it is phrased.
For example:
int MyFunction(nType){
//an "if" statement with a logical OR inside counts as 2 paths
since it's functionally equivalent of 2 "if" statements, each with it's
own half of the condition.
if ((nType == 0) || (nType == 255)){
nType = 1;
}
//A "switch" keyword doesn't
count as new path , since only the included "case" and "default"
statements cause new code paths.
switch(nType) {